En stämgaffel kommer nära, men förstärker den genom att placera den på något resonerande objekt - ett träbord, pianofodral eller prova ditt huvud :-) - kommer att lägga till några övertoner.

Det ljudproducerande elementet i ett Fender Rhodes elpiano är i huvudsak en stämgaffel, även om andra delar av instrumentet är utformade för att "smutsa upp" den rena tonen.

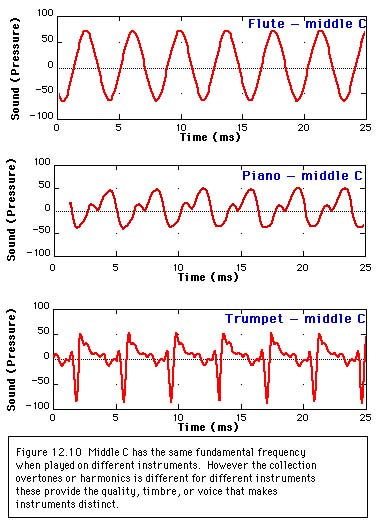
Tonen på en flöjt, särskilt i det högre registret, är nära en sinusvåg.

Observera att vi pratar om en hålls del av en ton. Både stämgaffel och flöjt producerar mycket mer komplexa ljud när en ton attackeras. Du kan misstänka en stämgaffel för en flöjt om attackdelen av en lapp huggs av. Jag tror inte att du skulle förväxla de två om attacken också hördes!

Denna princip användes bra i "Hybrid Synthesisers" som Roland D50 eller Yamaha SY-serien. En kort samplad attack följdes av en syntetiserad sustain och release. Det kombinerade en anmärkningsvärd grad av realism och kontrollerbarhet med ekonomisk användning av provminne.

Så ditt svar är: även om vissa instrument har en hållfasthet nära en sinusvåg kan jag inte tänka på ett utanför testet bänk som saknar en mer komplex attack.

Jag har hört det hävdas att mänskligt visselpipa kommer mycket nära att vara en perfekt sinusvåg:

video här verkar bara visa en topp på spektrografen och stödja en nästan perfekt sinusformad vågform.

Såvitt jag vet skapar varje instrument övertoner. Vissa kanske tror att orörd slagverk inte har övertonat, men de producerar dem också.

Det finns dock några elektroniska instrument, såsom synthesizers (sinusvågor) som kan spelas utan att producera några övertoner, men alla akustiska instrument gör det.

Om jag stämmer kan ocarina vara instrumentet som kommer så nära som möjligt att skapa "inga övertoner". Faktum är att de skapar övertoner också, men på grund av sin form är övertonerna faktiskt många oktaver över huvudtonen.

Det är värt att titta på anledningen VARFÖR det finns så få instrument som producerar sinusvågor. Ur fysikens synvinkel är det uppenbarligen ganska svårt att göra en sinusvåg utan elektronik, men människor kunde ha försökt komma nära om de ville.

Det psykoakustiska svaret är att få försökte detta eftersom det inte låter intressant. Det är anmärkningsvärt att de flesta av de föreslagna exemplen är:

Ej designad för mänsklig underhållning (t.ex. tuning gaffel)
Designad som en del av något (t.ex. spelas med andra)
Designad med andra funktioner för att göra ljudet mer intressant (t.ex. theramin)

Ett instrument som kommer ganska nära är Stylophone. Detta producerar en sinusvåg - i teorin - helt enkelt för att detta var det billigaste ljudet att sikta på i ett elektroniskt instrument. Varje avvikelse från sinusvåg orsakas inte av estetiska överväganden, utan av en överdriven önskan om billighet i designbriefen. Det vill säga övertonerna orsakas helt av den billiga förstärkaren, den billiga högtalaren och det billiga plastfodralet.

andra frekvenser än den dominerande frekvensen för noten

Alla ändliga vågor har andra frekvenser än den dominerande frekvensen. Enstaka frekvens är endast möjlig för en sinusform som har hållits sedan evigt med konstant amplitud och kommer att fortsätta att göra det.

För alla ändliga vågor kommer du att kunna uppfatta (med ditt öra eller någon fysisk mätanordning) en bunt med angränsande frekvenser som visas i bilden som ingår i ett annat svar. Buntens bredd är begränsad av signalens varaktighet.

OBS: Detta svar diskuterar inte övertoner i den vanliga innebörden av termen (multipel av grundfrekvens) utan definitionen från frågan (citerad ovan ).

Du kan skapa ren en sinusvåg med vissa elektroniska generatorer. Ett annat sätt är att använda programvara. Jag skapade en serie rena sinusvågor i wav-filer vid olika frekvenser för ett hörselprov. De låter inte som något riktigt instrument som jag någonsin har hört. Så det säger att inget instrument som jag har hört producerar en ren sinusvåg. Naturligtvis har jag inte hört alla instrument men jag har hört många. Det närmaste kan vara en flöjt men det var ändå igenkännligt annorlunda. Jag tycker inte att en ren sinusvåg är tilltalande.

Observera att skillnaden mellan ljudet från olika instrument är mer än övertonerna: t.ex. attack, förfall, tonhöjdsstabilitet osv. Tillbaka på kassettbandens dagar hade jag ett band av pianomusik som sträckte sig illa. Det lät inte längre alls som ett piano, det lät som en musiksåg. Övertonerna skulle inte ha förändrats (mycket) av sträckningen. Det indikerade att en väsentlig del av pianoljudet är tonhöjningens stabilitet. Av den anledningen har jag sedan dess alltid använt solo-pianomusik för att bedöma skivspelare. Det är länge sedan jag gjorde det, eftersom jag omedelbart konverterade till CD-skivor. Delvis på grund av denna erfarenhet.

Det finns redan ett stort antal "instrument" listade i andra svar men jag tror att en delmängd av organ kan återge en sinusformad ungefärlig.

På den elektriska sidan av sakerna använde Hammond-orgeln ett snurrande tonhjul och en elektrisk pickup för att generera nära sines. Varje tangent hade flera hjul som snurrade på multiplar av grundfrekvensen. Du kan justera ventiler som styr styrkan (amplituden) för varje överton - en tidig prototyp av additiva syntar. Därför kommer jag att hävda att Hammond-orgelet, till skillnad från andra instrument, var designat med sinusformad produktion i åtanke. Du kan också hävda att Hammond helt enkelt var ett försök att replikera den fullständiga känslan av äkta rörorgan. ¹ En live demonstration av finns på youtube (med tillhörande spektrogram) .

Det finns också det ursprungliga Telharmonium, en gigantisk maskin i fabriksstorlek som tillverkades nära sines på liknande sätt.

På Aerofon -sidan finns det vissa rör som är mycket sinusformade inklusive Tibia-rören som du kan höra lite under de första 30 sekunderna av detta video.

^{1 _{Du kan också hävda att Hammond helt enkelt var ett försök att replikera den fullständiga känslan av äkta rörorgan.}}

Se även lasso d'amore där referens anges "tonerna i tonerna [...] är" nästan alla grundläggande ", enligt Fourier-analys (liknar sinusvågor) . " Det är möjligt att spela instrumentet med en hastighet så nära övergången från en resonans till en annan att två samtidiga tonhöjder produceras. (Detta tenderar att vara möjligt vid högre hastigheter, där det är svårt att förhindra att olika hastigheter i olika bågar av armrörelsen producerar olika toner från varje båge.)

En ren sinusvåg är det enda instrumentet som spelar en ton utan övertoner. Det här är inte konstigt. Ett instruments klang är konsekvensen av dess unika övertoner - vilka det har, vilka som är högst, oavsett om vissa övertoner är något platta eller skarpa, och hur övertonerna muterar över tiden. Eftersom det bara finns en klangprofil som kan komma från att inte ha några övertoner, borde det inte bli en överraskning att det bara finns ett ljud som passar räkningen. Och när du tar bort alla övertoner från en ljudvåg är en sinusvåg precis vad du får.

Jag är ingen expert på det här, men här är min bästa bild.

Timbre är resultatet av en specifik serie övertoner som låter högre än andra. Vi letar efter en klang som bara har det grundläggande ljudet av och inget som låter ovanför det. Jag antar att allt som kan producera en enda sinusvåg skulle vara ditt svar. Kanske ett orgel med bara en ton som låter?